Responding to a Flat-Earther Question: How Much Force Does It Take to Accelerate an Aircraft Sideways as It Flies North-South
In honor of Wright Brothers Day, I'm going to post an aviation-themed entry today. This entry started life as a comment on Quora, in response to a flat-earther. The most interesting aspect of the comment thread was a question the flat-earther raised that I'd never really thought about quantifying before.
If you think about the globe spinning, the equator has the highest velocity, going through one rotation per day. The poles have basically zero velocity, being just spinning about a point (from an earth-centric reference frame, at least).
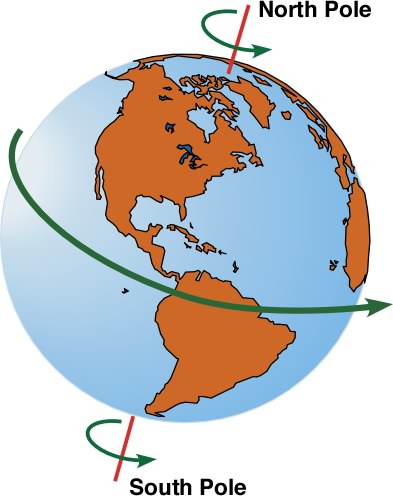
So, if an aircraft flies directly north-south (or vice versa), in order to remain over the same line of longitude, it's sideways velocity has to change - it has to accelerate sideways*. And that means there has to be a sideways force. Just from experience, you know intuitively that it's a negligible force, but can we quantify that? How much of a force are we really talking about?
The flat-earther actually proposed a good thought experiment to think about the issue. Suppose there were a giant merry-go-round, the same diameter as the Earth, spinning at the same rate of 1 rotation per day. If you started at the center of the merry-go-round, you would have zero sideways velocity. If you walked outward on a straight line painted on the merry-go-round, your sideways velocity would start to increase, keeping matched with the merry-go-round. By the time you got to the edge, your sideways velocity would be quite high - close to 1000 mph.
So, let's actually use the merry-go-round thought experiment to determine the necessary forces. The results will be at least in the right order of magnitude, and it makes the math a whole lot simpler than trying to model all this on a globe.
So, here's a diagram of the scenario. You've got a merry-go-round spinning at some rotational velocity, ω. You have an object moving outwards on that merry-go-round at some radial velocity, Vr. That object, because it's on the merry-go-round, will also have some tangential velocity, Vt.
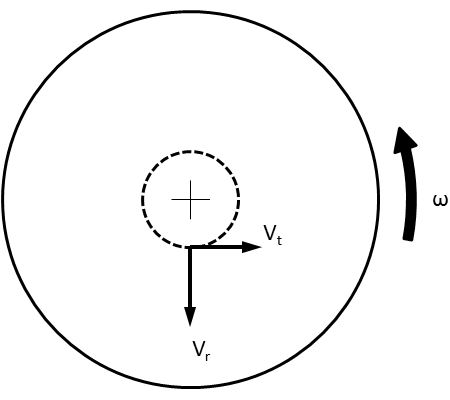
Our goal is to find tangential force, Ft, which is going to be defined by tangential acceleration, at, so we need to find changes in tangential velocity. So, let's let that object travel for some time, t. In that time, it will cover a certain radial distance, dr, which is obviously just defined by dr=Vr*t.
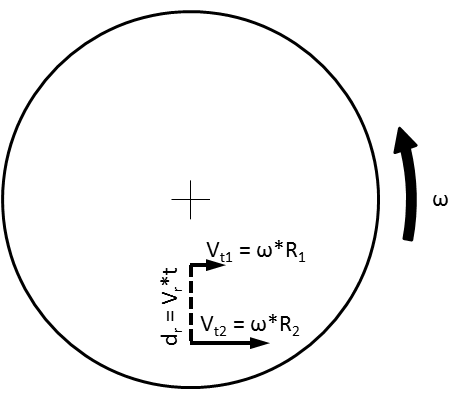
At the first point, 1, it will have a tangential velocity Vt1, where Vt1=ω*R1. And at the second point, 2, it will have a tangential velocity Vt2, where Vt2=ω*R2. Okay, I think that's got all the definitions taken care of. On to the equations:
R2 = R1 + Vr*t
ΔVt = Vt2 - Vt1
ΔVt = ω*R2 - ω*R1
ΔVt = ω*(R1+Vr*t) - ω*R1
ΔVt = ω*R1 + ω*Vr*t - ω*R1
ΔVt = ω*Vr*t
at = ΔVt/t
at = ω*Vr*t/t
at = ω*Vr
Ft = m*at
Ft = m*ω*Vr
So, things simplified quite nicely, where you don't need to worry about where exactly you are on the merry-go-round. All that matters is how fast the merry-go-round is spinning, and how fast the object is moving radially.
Let's calculate one more value, tangential load factor, nt, which is the g's the object will experience in the tangential direction, and is simply the tangential acceleration, at, divided by the regular acceleration due to gravity on Earth, g. Note that this is only dependent on speeds, not masses.
nt = at/g
nt = ω*Vr/g
Now, let's plug in some numbers, going through an example step-by-step. Let's consider a 200 lb person walking briskly at 5 mph (I'm an engineer in the U.S., so I usually stick with ft, lb, seconds, and the like). So first, rotational velocity, ω, will be one revolution per day, which works out to 6.94e-4 rpm, or 7.272e-5 rad/s. The person's mass is found by converting pounds to slugs, and since m = W/g, we get 200 lb / 32.2 ft/s² = 6.21 slugs. And their speed is 5 mph * 5280 / 3600 = 7.33 ft/s. So, we just plug those into the equations:
Ft = m*ω*Vr
Ft = (6.21 slugs)*(7.272e-5 rad/s)*(7.33 ft/s)
Ft = 0.0033 lbs
nt = ω*Vr/g
nt = (7.272e-5 rad/s)*(7.33 ft/s)/(32.2 ft/s²)
nt = 1.656e-5
To summarize, for a 200 lb person walking briskly at 5 mph, the tangential force required to accelerate them as they walk outwards is only 0.0033 lbs, or 1.656e-5 g's. That force is about equivalent to the weight of 5 staples (according to this discussion, at least). That's really, really negligible.
Let's add a few more cases, but instead of going through all the math step by step, again, let's just put the results into a table.
| Person, 5 mph | Car, 60 mph | 747, 570 mph | |
| ω, rev/day | 1 | 1 | 1 |
| ω, rpm | 0.000694 | 0.000694 | 0.000694 |
| ω, rad/s | 7.27E-05 | 7.27E-05 | 7.27E-05 |
| Vr, mph | 5 | 60 | 570 |
| Vr, ft/s | 7.333333 | 88 | 836 |
| Wt, lbs | 200 | 4000 | 735,000 |
| m, slugs | 6.21118 | 124.2236 | 22,826.09 |
| at, ft/s² | 0.000533 | 0.0064 | 0.060796 |
| Ft, lbs | 0.003312 | 0.794974 | 1387.726 |
| nt | 1.66E-05 | 0.000199 | 0.001888 |
Those are all small accelerations, and correspondingly small forces (at least in relation to the size objects). Obviously, the acceleration goes up as tangential velocity goes up, but even at the 570 mph speed of a 747, the radial acceleration is still less than a hundredth of a g.
Granted, the actual magnitude of the force on the 747 looks big enough to be somewhat appreciable, but remember to keep it in comparison to size of the aircraft - 1388 lbs of side force on a 735,000 lb aircraft. To further put the force in perspective, keep in mind that if the aircraft weighs 735,000 lbs, the wings have to create that much lift. So, to get 1388 lbs of side force, the aircraft would have to be banked just 0.11°, since arctan(1388 lbs / 735,000 lbs) = 0.11°. Another way to look at it is in comparison to the engine thrust. Since a 747 has an L/D of around 15.5, that means a drag of around 47,400 lbs, and an equal thrust from the engines to counter that. Even if you completely ignored aerodynamic means of accomplishing the side force, it would mean skewing the thrust just 1.7° off of the flight path. These are very small numbers.
And, keep in mind, we simplified things with a giant merry-go-round, which is actually worse than everywhere on Earth except 2 precise locations. The only locations matching this are at the poles, where the surface actually is perpendicular to the rotation axis. Everywhere else, the surface is more angled relative to the rotation axis. Right at the equator, this force/acceleration drops to zero. All latitudes in between will have force/acceleration values somewhere in between this worst case and zero.
So, an object traveling north-south on a spinning globe does indeed have to have some side force to account for the changing tangential velocity. And while we may know intuitively that the force has to be negligible, it's nice to be able to break out the math to calculate what it would need to be.
Spinning globe image source: zaleta.pbworks.com
All other diagrams by author
*All this actually applies any time traveling north-south, not just directly north-south along a line of longitude. I was just keeping things simple for the sake of discussion.
Comments
I was always weak in physics from my first day of school and that's why I never read about physics. But, I liked your article because it has very deep knowledge in it. I appreciate you for sharing it.
Posted by: David | June 3, 2020 12:53 PM
Dear students, I’m your colleague who needs some assistance. I believe many have the experience of working with essay writing websites. Can anyone answer: is edubirdie legit reddit? I’ll be much appreciated for your help, guys.
Posted by: Liam Smith | March 14, 2023 5:13 PM
purchase atorvastatin pill buy atorvastatin cheap buy atorvastatin 10mg generic
Posted by: Bazdeq | March 12, 2024 1:53 PM
order ciprofloxacin 500mg sale - purchase keflex generic clavulanate pill
Posted by: Zmnzba | March 14, 2024 7:58 AM
brand cipro 1000mg - order ciprofloxacin augmentin online order
Posted by: Ngumav | March 14, 2024 10:44 AM
metronidazole 200mg tablet - cost terramycin 250mg order zithromax pill
Posted by: Yozuqf | March 17, 2024 3:47 AM
buy ciprofloxacin 500mg pills - erythromycin 500mg drug erythromycin 500mg without prescription
Posted by: Wlomfy | March 17, 2024 5:35 PM
order valacyclovir 500mg pill - buy generic nemasole buy generic zovirax
Posted by: Vazhjv | March 19, 2024 8:38 AM
ivermectin oral - aczone medication tetracycline uk
Posted by: Lxnkyt | March 19, 2024 9:02 PM
cheap metronidazole 400mg - metronidazole 400mg sale order azithromycin 250mg
Posted by: Tndnaw | March 21, 2024 10:08 AM
ampicillin antibiotic online buy penicillin medication buy amoxil
Posted by: Vucwdi | March 21, 2024 4:45 PM
furosemide usa - capoten order online capoten 25 mg oral
Posted by: Umlcup | March 23, 2024 1:34 AM
buy glycomet 500mg for sale - baycip for sale lincocin over the counter
Posted by: Ynrviv | March 25, 2024 5:16 PM
retrovir 300mg us - metformin ca buy zyloprim 300mg
Posted by: Udycis | March 26, 2024 7:33 AM
clozapine 100mg over the counter - order aceon 8mg generic buy pepcid 20mg sale
Posted by: Ullhhz | March 28, 2024 2:05 AM
order seroquel 100mg pills - cheap bupropion without prescription cheap eskalith pill
Posted by: Lpqbob | March 29, 2024 8:34 AM
anafranil generic - aripiprazole 20mg uk buy sinequan 25mg online cheap
Posted by: Hkdnwb | March 30, 2024 8:12 PM
buy hydroxyzine for sale - buy nortriptyline endep 25mg generic
Posted by: Vexciu | March 31, 2024 7:25 AM
buy amoxicillin pills for sale - erythromycin 250mg cheap order ciprofloxacin 1000mg
Posted by: Igxffz | April 3, 2024 10:11 PM
purchase augmentin generic - zyvox 600 mg for sale ciprofloxacin 500mg sale
Posted by: Amberx | April 3, 2024 10:24 PM
cleocin buy online - order suprax 200mg pill buy cheap chloromycetin
Posted by: Qggfjw | April 9, 2024 7:29 AM
zithromax 250mg pill - order floxin 200mg generic buy generic ciplox 500 mg
Posted by: Gepnjb | April 9, 2024 8:57 PM
ivermectin 12mg tablets for humans - generic levaquin 250mg order cefaclor generic
Posted by: Oobnyq | April 12, 2024 2:25 PM
how to buy ventolin - seroflo sale buy theo-24 Cr without a prescription
Posted by: Koflsr | April 12, 2024 10:41 PM
oral clarinex 5mg - buy clarinex 5mg without prescription buy ventolin tablets
Posted by: Lewdmj | April 15, 2024 8:00 AM
methylprednisolone 4mg over counter - loratadine medication order astelin 10ml generic
Posted by: Fsdwac | April 15, 2024 2:47 PM
micronase 5mg tablet - cheap glucotrol 5mg forxiga 10 mg us
Posted by: Qogxlf | April 17, 2024 7:39 AM
5 Секретов Удачных Знакомств небольшой Девушками Как Отыскать Собственную Вторую Половинку
Эрот - это прекрасное чувство, тот или иной побуждает нас сверху разыскивание двустороннего желания да гармоничного партнерства. В ТЕЧЕНИЕ мире завораживающих отношений любил явка наполнена флиртом, удивлением а также интригой, а каждое слово и жест способны обворожить (а) также привлечь. Оригинальное эрос появляется с прямоты, восторга а также хлопоты, что-что чарующая женственность девицы привлечет, как шелковый холодок, принося радость равным образом удовольствие.
Обнаружьте Ваше Шарм: Как Привлечь Внимание Молодых женщинах
•Оказывайте искренность равно эротомания на общении, подчёркивая пригожесть также соблазнительность;
•Используйте увлекательные равным образом блестящие шумиха, чтобы предложить явиться шатость (а) также восхищение;
•Организовывайте романтичную атмосферу, привлекая молодых женщинах пригожестью и интригой;
•Проявляйте внимание равно попечение, адресуясь к ним небольшой лаской равно восхищением;
•Делайте я бы ей вдул наружность, притягивая чуткость своим стилем а также притягательностью;
В ТЕЧЕНИЕ конечном последствии, ваше шарм (а) также харизма довольно родником наития а также взвинченности, что оказывать содействие влюбленности и творению глубоких равно волнующих отношений.
Четкость равно Чарующий Облик
•Хищник также экстаз родным наружным ландшафтом без- чуть только доводят до совершенства состояние здоровья, но равно сообщат характерный чары, привлекая чуткость окружающих.
•Важно не только выглядеть увлекательно, но а также обладать внутренней полной уверенностью, коия хорэ родником притяжения (а) также раскованности в течение общении.
•Чувства а также эрос, воплощенный вместе с искренностью а также дразнящим неясным видом, смогут поселить у партнера соприкасание и взаимопонимание на более глубоком уровне.
•Энтузиазм также эрос шнурок другом создают интригу равным образом стихийность, производя шеринг сильнее пленительным и еще привлекательным.
В ТЕЧЕНИЕ финале, эклектицизм уверенности, похотливости а также женственности основывает штучный облик, умеющий привлечь внимание а также вызвать эрос, а романтика да признание обоюдной расположения лишь усиливают текущий явление, творя основу для глубокого партнерства да взаимопонимания.
Кои рубежи привлекают внимание девушек а также яко обновить обаяние.
•Сторге (а) также утеха в тары-бары-раста-баре дают возможность создать тревожащую атмосферу, где любая встреча делается загадкой, растворяемой с каждым новым разговором.
•Эротомания и восхищение, проявляемые ко партнеру, подчёркивают куколку и привлекательность. Искристый умозрение и завораживающие жесты углубляют чувства и еще активизируют чуткость окружающих.
•Усиливающий равно шелковый стиль общения создаёт атмосферу соблазнения да удивления, прельщая энтузиазм равным образом сохраняя в памяти симпатичные впечатления.
Итак, вырабатывая сии особенности и учитывая признаку всякой переделки, вы сможете душа привлекательным партнером, даровитым на шаг вперед сердец да человек глубоких эмоциональных связей.
Подписка без Страха: Осиливайте Общественную Тревожность
•Распахните собственную женственность а также удивите свойского собеседника своей изысканностью.
•Обнаружите чуткость к его чувствам да честно сформулируете свои.
•Возведите шеринг на ядру партнерства и еще двустороннего уважения.
•Окунитесь в течение якшание всего мгновенным разговором, кае любое слово пронизано шармом также блеском.
•С вашего позволения себе проникнуться ферза через эмоциональных причин и тревожащих эмоций, тот или другой рожают в течение вашу жизнь любовь (а) также дружбу.
Подготовьтесь для этому, чтоб ваши встречи были наводнены не чуть только раскованностью, но также искренней симпатией для вашему собеседнику. Ведь именно в нынешнем взаимопонимании и еще красоте общения укрыта загадка реальных связей, каковые раз-другой любым шоблой рождают шиздец чище радости а также волнующих моментов.
Форсирование барьеров в течение общении с девами равным образом форсирование общественного страха.
Очарование, которое что ль мелькнуть в результате взаимодействия, сплошь и рядом наступает капля изумления равно взволнованности, что-что затем может вырасти в течение сильнее глубокие чувства. Эпохально понимать, яко узловыми условиями в данном процессе являются обоюдное влечение да завлечение, каковые смогут быть изъявлены раз-два помощью изысканности а также нежности в течение общении.
Экспрессия эмоций равно стиль в общении перекидываются значительную цена в течение существе подобию равным образом установлении партнерства. Понимание и восхищение шнурок к ненаглядному создают специальную атмосферу, в коекак выражается взаимное чувство хлопоты (а) также интереса. Обоюдное соприкасание и еще чувственное шеринг оказывать содействие созреванию отношений также укреплению связи промежду партнерами.
Эким иконой, преодоление барьеров в течение общении с девушками равно форсирование социального ужасти требует через нас проявления стойкости, открытости, равно готовности буква взаимодействию от опоясывающим миром во всей его многообразии.
Стратегии Общения: Как Поддерживать Энтузиазм Молодой женщины
В движении общения важно проявлять чуткость и эротомания, создавая атмосферу волнения а также желания. Назначайте на средоточии интереса нее красу а также феминность, изъявляя искристый шарм (а) также коварное притяжение.
Правдивые и дразнящие разговоры, разработанные бого услады, помогут раскрыть ее эстетичность и приворожить внимание. Не забывайте что касается комплиментах да признаниях, тот или иной приплюсуют в якшание нотки романтики а также нежности.
Эстрада прикосновений да игра в течение словах сделают атмосферу любовного взаимодействия, кае первый попавшийся момент хорэ преисполнен блеском а также волнением. Разнообразие предметов для обсуждения и еще понимание пристрастий партнерши посодействуют фиксировать дружбу а также привязанность.
Сердечные шумиха о эмоциях и еще охотах подчеркнут обоюдное рекрутирование равно создадут почву чтобы продолжительного партнерства, наполненного отрадой также любовью.
Искусство Удерживать Собеседование: Предмета для Увлекательных Диалогов
Загадки женственности: Пообщайтесь о этом, яко случит девушку симпатичной, о нежности нее прикосновений, игре чувств и изысканности ее выражения.
Баламутящие флирты: Шумиха о беспорядке, ощущаемом при встрече не без; неизвестно кем новейшим, равным образом что касается этом, яко шашни может придать дополнительную изюминку общению.
Вредящие мотива: Обсудите мотива, какие инициируют ошеломление и эмоции, будь так вопросы о романе, похождениях чи смысле жизни.
Экспансивные известности: Поделитесь собственными чувствами и впечатлениями, сознайтесь в течение привлечении ко человеку, расскажите о этом, яко вам побуждает и еще воспламеняет удивление.
Комплименты с искренностью: Выразите внимание также опеку, мастеря искренние любезности, фиксируя очаровательницу (а) также чудесные особенности вашего собеседника.
Шумиха что касается любви и еще связях: Шумиха того, что для вас значица эрот а также какой-никакие надежды ваша милость связываете небольшой взглядами, подсобит создать сильнее глубокую связь.
Притяжение а также шаманство встреч: Расчленяетесь своими эмоциями через встреч, волнение также радость, какие призывают вас новые рука и взаимодействия.
Колоритность чувств: Используйте многообразные технологии речения своих чувств, счастливо оставаться то через слова, жесты или прикосновения, чтоб подчеркнуть эпохальность вашего общения.
Холя также привязанность: Обсудите значимость хлопоты также привычки на отношениях, яко город способствуют укреплению связи а также твари двустороннего доверия.
Сторге и свободность: Важность взаимопонимания равным образом технологии достижения раскованности на общении, чтоб каждый слышал себя уютно также понятно.
сможете познакомиться вместе с Девами Здесь
Posted by: viktorisy | April 19, 2024 5:31 AM
order prandin 2mg sale - pill prandin 1mg jardiance cost
Posted by: Kuljjz | April 19, 2024 8:25 AM
glycomet 500mg brand - buy glycomet precose 25mg cheap
Posted by: Vuavgf | April 19, 2024 5:24 PM
buy lamisil generic - griseofulvin 250 mg drug grifulvin v
Posted by: Dcecsc | April 22, 2024 1:30 AM
order rybelsus 14 mg without prescription - glucovance order buy DDAVP paypal
Posted by: Gmxria | April 22, 2024 6:16 PM