On December 17th, 1903, the Wright Brothers, Orville and Wilbur, became the first people to achieve an accomplishment that people had been dreaming of for millenia - controlled, powered flight. Now, they weren't lone geniuses working in a vacuum. Others had had earlier limited successes, and people would have figured everything out eventually even without the Wrights (and were largely on the path to doing so, since the Wrights kept so much of their own research a secret), but the Wright brothers had a systematic, logical approach, putting them years ahead of their contemporaries. When they gave their first public demonstrations in France in 1908, crowds were awestruck. They certainly deserve the honor of being the first to flight.

To quote myself from a previous entry, "Flying has become so common place today that we take it for granted. People complain about the cramped seats, the long lines to get through security, the bad food (if you even get any) on flights. But just remember how long people have dreamt of flight, for how long people looked to the skies wanting to emulate the birds. Flying used to be the stuff of myth and legends, reserved for the gods. Now, we can all get in an airplane, and soar above the clouds. It really is something special."

Here are a few of the better aviation related pages/entries on this site that would make for good reading for Wright Brothers Day. The first entry on the last is brand new today.

• Responding to a Flat-Earther Question: How Much Force Does It Take to Accelerate an Aircraft Sideways as It Flies North-South - Goes through the derivation of the formulas for a simple estimate of the answer to the question in the title. It's a negigible force, but still interesting to figure out.
   
• Did Gustave Whitehead Beat the Wright Brothers as the First To Fly - There seems to be a perennial claim that Gustave Whitehead deserves the credit as the first person to fly. And while he did do some early experiments, the available evidence indicates that he wasn't particularly successful. There's an especially interesting rebuke of a photo claimed to show Whitehead in flight.
   
• My Favorite Airplanes - Exactly what it sounds like - my top 10 favorite airplanes, with photos and short descriptions.
   
• A Plane Christmas Greeting - This is a poem written by my late Uncle Bud. We both shared a love of aviation. This is his version of "The Night Before Christmas", with an aviation twist.
   
• Instructions to fold a Post-It Note Glider - Instructions to fold a glider from a Post-It Note that actually works surprisingly well. It even got picked up and included in a book celebrating the Post-It Note's 25th anniversarry.
   
• Flying - A short ode to flying, and why it's still such a marvel even now that it's commonplace.

So as you go about your business today, take a moment to look up and find an airplane, and marvel a little at the achievement.

Much of the content of this entry was recycled, sometimes verbatim, from previous Wright Brothers Day entries.

Posted by Jeff on Monday, Dec 17 | Permalink | Comments (45) | TrackBacks (0)

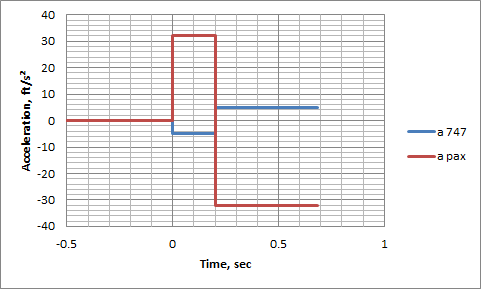
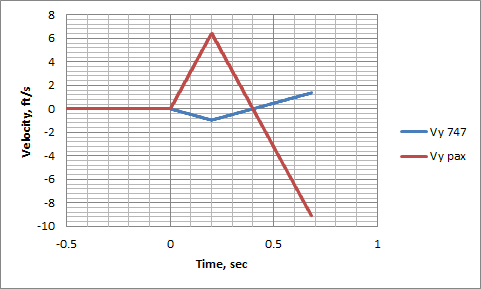
In honor of Wright Brothers Day, I'm going to post an aviation-themed entry today. This entry started life as a comment on Quora, in response to a flat-earther. The most interesting aspect of the comment thread was a question the flat-earther raised that I'd never really thought about quantifying before.

If you think about the globe spinning, the equator has the highest velocity, going through one rotation per day. The poles have basically zero velocity, being just spinning about a point (from an earth-centric reference frame, at least).

So, if an aircraft flies directly north-south (or vice versa), in order to remain over the same line of longitude, it's sideways velocity has to change - it has to accelerate sideways*. And that means there has to be a sideways force. Just from experience, you know intuitively that it's a negligible force, but can we quantify that? How much of a force are we really talking about?

The flat-earther actually proposed a good thought experiment to think about the issue. Suppose there were a giant merry-go-round, the same diameter as the Earth, spinning at the same rate of 1 rotation per day. If you started at the center of the merry-go-round, you would have zero sideways velocity. If you walked outward on a straight line painted on the merry-go-round, your sideways velocity would start to increase, keeping matched with the merry-go-round. By the time you got to the edge, your sideways velocity would be quite high - close to 1000 mph.

So, let's actually use the merry-go-round thought experiment to determine the necessary forces. The results will be at least in the right order of magnitude, and it makes the math a whole lot simpler than trying to model all this on a globe.

So, here's a diagram of the scenario. You've got a merry-go-round spinning at some rotational velocity, ω. You have an object moving outwards on that merry-go-round at some radial velocity, V_r. That object, because it's on the merry-go-round, will also have some tangential velocity, V_t.

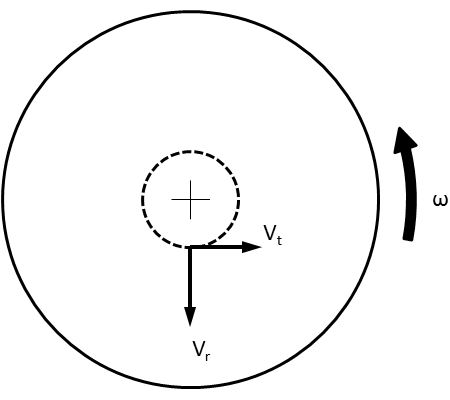
Our goal is to find tangential force, F_t, which is going to be defined by tangential acceleration, a_t, so we need to find changes in tangential velocity. So, let's let that object travel for some time, t. In that time, it will cover a certain radial distance, d_r, which is obviously just defined by d_r=V_r*t.

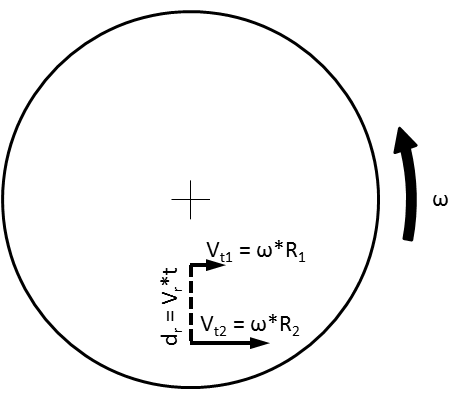
At the first point, 1, it will have a tangential velocity V_t1, where V_t1=ω*R₁. And at the second point, 2, it will have a tangential velocity V_t2, where V_t2=ω*R₂. Okay, I think that's got all the definitions taken care of. On to the equations:

R₂ = R₁ + V_r*t

ΔV_t = V_t2 - V_t1
ΔV_t = ω*R₂ - ω*R₁
ΔV_t = ω*(R₁+V_r*t) - ω*R₁
ΔV_t = ω*R₁ + ω*V_r*t - ω*R₁
ΔV_t = ω*V_r*t

a_t = ΔV_t/t
a_t = ω*V_r*t/t
a_t = ω*V_r

F_t = m*a_t
F_t = m*ω*V_r

So, things simplified quite nicely, where you don't need to worry about where exactly you are on the merry-go-round. All that matters is how fast the merry-go-round is spinning, and how fast the object is moving radially.

Let's calculate one more value, tangential load factor, n_t, which is the g's the object will experience in the tangential direction, and is simply the tangential acceleration, a_t, divided by the regular acceleration due to gravity on Earth, g. Note that this is only dependent on speeds, not masses.

n_t = a_t/g
n_t = ω*V_r/g

Now, let's plug in some numbers, going through an example step-by-step. Let's consider a 200 lb person walking briskly at 5 mph (I'm an engineer in the U.S., so I usually stick with ft, lb, seconds, and the like). So first, rotational velocity, ω, will be one revolution per day, which works out to 6.94e-4 rpm, or 7.272e-5 rad/s. The person's mass is found by converting pounds to slugs, and since m = W/g, we get 200 lb / 32.2 ft/s² = 6.21 slugs. And their speed is 5 mph * 5280 / 3600 = 7.33 ft/s. So, we just plug those into the equations:

F_t = m*ω*V_r
F_t = (6.21 slugs)*(7.272e-5 rad/s)*(7.33 ft/s)
F_t = 0.0033 lbs

n_t = ω*V_r/g
n_t = (7.272e-5 rad/s)*(7.33 ft/s)/(32.2 ft/s²)
n_t = 1.656e-5

To summarize, for a 200 lb person walking briskly at 5 mph, the tangential force required to accelerate them as they walk outwards is only 0.0033 lbs, or 1.656e-5 g's. That force is about equivalent to the weight of 5 staples (according to this discussion, at least). That's really, really negligible.

Let's add a few more cases, but instead of going through all the math step by step, again, let's just put the results into a table.

Those are all small accelerations, and correspondingly small forces (at least in relation to the size objects). Obviously, the acceleration goes up as tangential velocity goes up, but even at the 570 mph speed of a 747, the radial acceleration is still less than a hundredth of a g.

Granted, the actual magnitude of the force on the 747 looks big enough to be somewhat appreciable, but remember to keep it in comparison to size of the aircraft - 1388 lbs of side force on a 735,000 lb aircraft. To further put the force in perspective, keep in mind that if the aircraft weighs 735,000 lbs, the wings have to create that much lift. So, to get 1388 lbs of side force, the aircraft would have to be banked just 0.11°, since arctan(1388 lbs / 735,000 lbs) = 0.11°. Another way to look at it is in comparison to the engine thrust. Since a 747 has an L/D of around 15.5, that means a drag of around 47,400 lbs, and an equal thrust from the engines to counter that. Even if you completely ignored aerodynamic means of accomplishing the side force, it would mean skewing the thrust just 1.7° off of the flight path. These are very small numbers.

And, keep in mind, we simplified things with a giant merry-go-round, which is actually worse than everywhere on Earth except 2 precise locations. The only locations matching this are at the poles, where the surface actually is perpendicular to the rotation axis. Everywhere else, the surface is more angled relative to the rotation axis. Right at the equator, this force/acceleration drops to zero. All latitudes in between will have force/acceleration values somewhere in between this worst case and zero.

So, an object traveling north-south on a spinning globe does indeed have to have some side force to account for the changing tangential velocity. And while we may know intuitively that the force has to be negligible, it's nice to be able to break out the math to calculate what it would need to be.

Spinning globe image source: zaleta.pbworks.com
All other diagrams by author

*All this actually applies any time traveling north-south, not just directly north-south along a line of longitude. I was just keeping things simple for the sake of discussion.

Posted by Jeff on Monday, Dec 17 | Permalink | Comments (44) | TrackBacks (0)

I recently came across the Quora question, If everybody on a Boeing 747 jumped at the same time, what would happen to the plane?. The first answer I read was spectacularly wrong, and most of the others were either guesses, jokes, or just generalities without much substance. So, I did what any good engineer would do and calculated it. Here's what I wrote.

In general - not much is going to happen if everybody on a 747 jumps at the same time. Just from a big picture view - there is no major change to the external forces acting on the aircraft/passenger system. So, you would expect the combined center of gravity to continue along the same path. And since most people can't jump very high, and the aircraft weighs substantially more than the passengers, the aircraft isn't going to be affected much at all.

In general, when the passengers jump, they'll push the aircraft down slightly, in proportion to their own mass and how far they jumped up. Then, since the lift didn't go away on the aircraft, the lift will first slow down the aircraft's slight descent, then cause the aircraft to start to climb again as the passengers start to fall.

But we don't have to just hand-wave an answer. We've got equations - we can calculate what will happen. So, I made a super simple model of this, with one mass to represent the aircraft, and another to represent the passengers*.

According to Wikipedia, a 747-400ER can hold 660 passengers, and has max takeoff weight of 910,000 lbs. According to FAA Advisory Circular 120-27E, average adult passenger weight in the winter, including "a 16-pound allowance for personal items and carry-on bags" is 195 lbs. Assuming the plane is full of adults, and that they're not going to be holding their carry-ons when they jump, that's 179 lbs per passenger, or a total of 118,140 lbs for all the passengers combined. That leaves 791,860 lbs for the aircraft itself.

For the forces, I assumed that the passengers jumping would be applying a constant force 2x their weight for 0.2 seconds. For the lift on the 747, I assumed that it would remain unchanged. Granted, there will be a small change in angle of attack (not pitch) due to the changes in vertical velocity, but I assumed it would be negligible.

So, what actually happens? This:

For passengers jumping ~1.3 ft into the air, the airframe itself will dip ~0.2 ft (2.4 in). Unsurprisingly - that's the same ratio as passenger weight to aircraft weight (confirming that the combined center of gravity does indeed continue on the same path unaltered). As the passengers reach the apex of their leap, the 747 reaches the bottom of its dip, and they quickly come back in contact again in less than a second.

I did skip out on what happens when they come back in contact, since I only did a super simple model and didn't really feel like spending a lot of time on it. They won't come smacking into each other. Rather, it'll probably be something like a mirror image of the jump, where the passengers flex their legs as they land to cushion the coming back together.

And of course, if you change up the assumptions, this will all change accordingly, but this puts the whole thing into perspective, showing the magnitudes and general behavior.

*Here's a fuller description of the simple model, attempting to put it terms that most people can understand. Like I said, I broke the system up into 2 bodies - one for the 747, and one for the passengers. Here's a diagram of the forces acting on each body (insert joke about spherical cows here):

Note first of all that I'm only looking at forces in the vertical direction, since that's the only thing changing in this problem. Thrust and drag are staying constant, so the speed of the aircraft isn't going to change. Next, note that thanks to Newton's Third Law, we know that the force the passengers are pushing down on the 747 is the same magnitude but in the opposite direction as the force that the 747 is pushing up on the passengers. That's the magenta arrow on each body. Finally, note that that's the only force that changes during the entire problem. The weight of the aircraft is essentially constant. The weight of the passengers is essentially constant. And like I already explained up above, I assumed that the lift remained constant. So, here are graphs of what those forces look like, with an additional solid curve showing the net forces on each body (or the summation of forces, designated with the Σ label):

Note that just before the jump, everything was in equilibrium, with no net forces. As the passengers jumped, they pushed down on the plane. Once they were in the air, that force, Fy_pax_to_747, went to zero, and then only lift and gravity were acting on the 747, and only gravity was acting on the passengers.

Next, we use Newton's second law, F=ma, to figure out the accelerations on the bodies. Since the force of the passengers jumping was modeled so simply as a constant force for 0.2 seconds, and all other forces were constant, the accelerations also all turned out to be constant.

For a constant acceleration, it's easy to calculate velocity, using the formula V2 = V1 + a*Δt. That produces accelerations over time that look like:

Finally, I used the velocities to calculate how far the bodies moved. I actually broke it up into 0.001 second increments, and did this linearly, with the simple formula h2 = h1 + V*Δt. That's not exactly accurate when velocity isn't constant. There are more exact formulas you can use, but when you break it up into such short segments, you're going to be very, very close. And with Excel, it's very easy to do this brute force approach. And doing that gave the graph I already showed up above, but which I'll repeat again here for completeness:

Image Source: NASA by way of Business Insider

Posted by Jeff on Friday, Jun 9 | Permalink | Comments (41) | TrackBacks (0)

113 years ago today, the Wright brothers became the first humans to truly fulfill the dream of flight. You can read what I wrote about the significance of this from my Wright Brother's Day, 2007 entry. On a related note, you could read my entry, Flying, from a few years ago, where I marvel at just how cool it really is to be able to fly.

(Yes, this entry is recycled. I only have my iPhone today, so I'm not up for typing a long original entry. But I still couldn't let the day go unmentioned.)

Posted by Jeff on Saturday, Dec 17 | Permalink | Comments (41) | TrackBacks (0)

On this day in 1903, the Wright brothers became the first people to achieve a dream of humanity for thousands and thousands of years - flying. Yes, their legend is a little overhyped in some circles. There were aviation pioneers who had preceded them, and contemporaries working on the problem at the same time who would have figured it out eventually, but the Wrights were the first. Moreover, with their systematic approach and especially with their focus on control, they were years ahead of everyone else. When they gave their first public demonstrations in France in 1908 (they'd spent that intervening time improving their flying machines), crowds were awestruck.

To quote myself from a previous entry, "Flying has become so common place today that we take it for granted. People complain about the cramped seats, the long lines to get through security, the bad food (if you even get any) on flights. But just remember how long people have dreamt of flight, for how long people looked to the skies wanting to emulate the birds. Flying used to be the stuff of myth and legends, reserved for the gods. Now, we can all get in an airplane, and soar above the clouds. It really is something special."

So as you go about your business today, take a moment to look up and find an airplane, and marvel a little at the achievement.

For more aviation-themed information on this site, you could browse the Aviation Archive on the blog, or check out the Aviation Section of my static pages. Or you could jump to some of the highlighted pages I've listed below.

Related Entries/Pages:

• Flying
• Did Gustave Whitehead Beat the Wright Brothers as the First To Fly
• My Favorite Airplanes
• A Plane Christmas Greeting
• Instructions to fold a Post-It Note Glider

Previous Wright Brothers Day Entries:

• 2007
• 2008
• 2010
• 2011
• 2013
• 2014

Posted by Jeff on Thursday, Dec 17 | Permalink | Comments (38) | TrackBacks (0)