Jeff's Lunchbreak: What Would Happn if Everybody on an Airliner Jumped at the Same Time?

Vomit Comet I recently came across the Quora question, If everybody on a Boeing 747 jumped at the same time, what would happen to the plane?. The first answer I read was spectacularly wrong, and most of the others were either guesses, jokes, or just generalities without much substance. So, I did what any good engineer would do and calculated it. Here's what I wrote.

---

In general - not much is going to happen if everybody on a 747 jumps at the same time. Just from a big picture view - there is no major change to the external forces acting on the aircraft/passenger system. So, you would expect the combined center of gravity to continue along the same path. And since most people can't jump very high, and the aircraft weighs substantially more than the passengers, the aircraft isn't going to be affected much at all.

In general, when the passengers jump, they'll push the aircraft down slightly, in proportion to their own mass and how far they jumped up. Then, since the lift didn't go away on the aircraft, the lift will first slow down the aircraft's slight descent, then cause the aircraft to start to climb again as the passengers start to fall.

But we don't have to just hand-wave an answer. We've got equations - we can calculate what will happen. So, I made a super simple model of this, with one mass to represent the aircraft, and another to represent the passengers*.

According to Wikipedia, a 747-400ER can hold 660 passengers, and has max takeoff weight of 910,000 lbs. According to FAA Advisory Circular 120-27E, average adult passenger weight in the winter, including "a 16-pound allowance for personal items and carry-on bags" is 195 lbs. Assuming the plane is full of adults, and that they're not going to be holding their carry-ons when they jump, that's 179 lbs per passenger, or a total of 118,140 lbs for all the passengers combined. That leaves 791,860 lbs for the aircraft itself.

For the forces, I assumed that the passengers jumping would be applying a constant force 2x their weight for 0.2 seconds. For the lift on the 747, I assumed that it would remain unchanged. Granted, there will be a small change in angle of attack (not pitch) due to the changes in vertical velocity, but I assumed it would be negligible.

So, what actually happens? This:

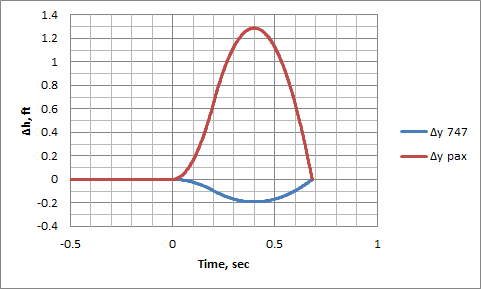
For passengers jumping ~1.3 ft into the air, the airframe itself will dip ~0.2 ft (2.4 in). Unsurprisingly - that's the same ratio as passenger weight to aircraft weight (confirming that the combined center of gravity does indeed continue on the same path unaltered). As the passengers reach the apex of their leap, the 747 reaches the bottom of its dip, and they quickly come back in contact again in less than a second.

I did skip out on what happens when they come back in contact, since I only did a super simple model and didn't really feel like spending a lot of time on it. They won't come smacking into each other. Rather, it'll probably be something like a mirror image of the jump, where the passengers flex their legs as they land to cushion the coming back together.

And of course, if you change up the assumptions, this will all change accordingly, but this puts the whole thing into perspective, showing the magnitudes and general behavior.

---

*Here's a fuller description of the simple model, attempting to put it terms that most people can understand. Like I said, I broke the system up into 2 bodies - one for the 747, and one for the passengers. Here's a diagram of the forces acting on each body (insert joke about spherical cows here):

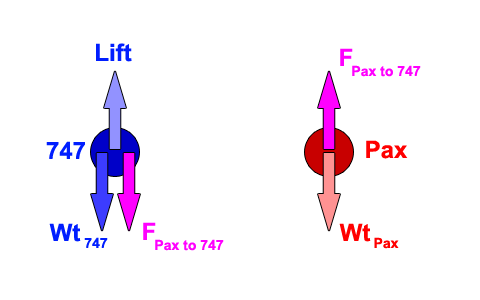
Note first of all that I'm only looking at forces in the vertical direction, since that's the only thing changing in this problem. Thrust and drag are staying constant, so the speed of the aircraft isn't going to change. Next, note that thanks to Newton's Third Law, we know that the force the passengers are pushing down on the 747 is the same magnitude but in the opposite direction as the force that the 747 is pushing up on the passengers. That's the magenta arrow on each body. Finally, note that that's the only force that changes during the entire problem. The weight of the aircraft is essentially constant. The weight of the passengers is essentially constant. And like I already explained up above, I assumed that the lift remained constant. So, here are graphs of what those forces look like, with an additional solid curve showing the net forces on each body (or the summation of forces, designated with the Σ label):

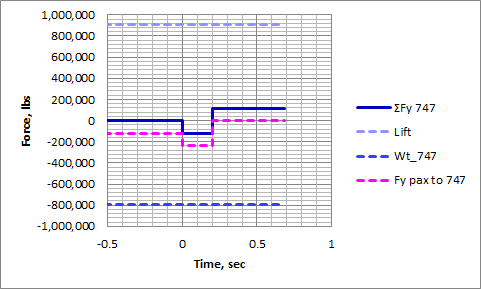
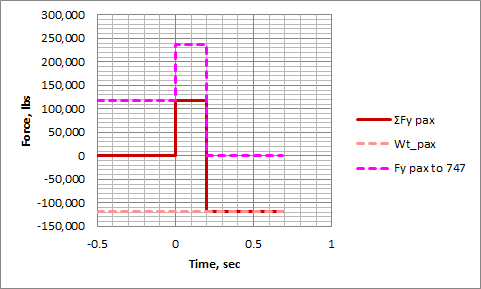
Note that just before the jump, everything was in equilibrium, with no net forces. As the passengers jumped, they pushed down on the plane. Once they were in the air, that force, Fy_pax_to_747, went to zero, and then only lift and gravity were acting on the 747, and only gravity was acting on the passengers.

Next, we use Newton's second law, F=ma, to figure out the accelerations on the bodies. Since the force of the passengers jumping was modeled so simply as a constant force for 0.2 seconds, and all other forces were constant, the accelerations also all turned out to be constant.

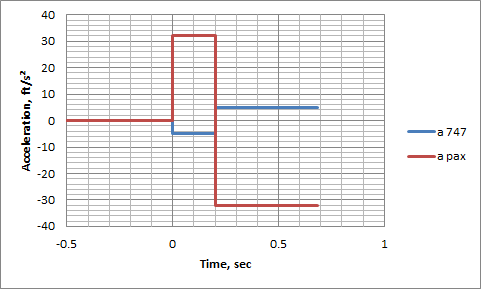
For a constant acceleration, it's easy to calculate velocity, using the formula V2 = V1 + a*Δt. That produces accelerations over time that look like:

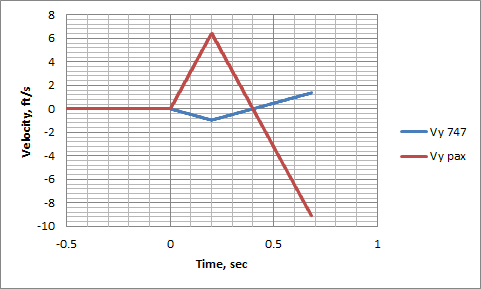
Finally, I used the velocities to calculate how far the bodies moved. I actually broke it up into 0.001 second increments, and did this linearly, with the simple formula h2 = h1 + V*Δt. That's not exactly accurate when velocity isn't constant. There are more exact formulas you can use, but when you break it up into such short segments, you're going to be very, very close. And with Excel, it's very easy to do this brute force approach. And doing that gave the graph I already showed up above, but which I'll repeat again here for completeness:

Image Source: NASA by way of Business Insider